Given the function:
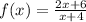
Let's graph the function.
To graph, let's first find the vertical and horizontal asymptotes.
To find the vertical asymptote, let's equate the denominator to 0 and solve for x.
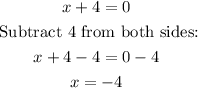
The vertical asymptote is:
x = -4
To find the horizontal asymptote, apply the condition:
n = m
Where n is the degree of the numerator while m is the degree of the denominator.
Since n = m, the horizontal asymptote will be:
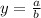
Where:
a = 2
b = 1
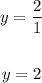
The horizontal asymptote is:
y = 2
We have a sketch of the asymptotes below:
Now, let's find two points each.
We have the following:
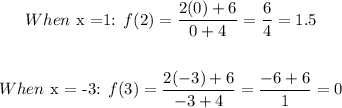
We have the points: (1, 1.5), (-3, 0)
Also find two points on the upper part:
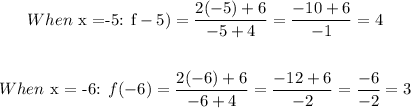
We have the points: (-5, 4) and (-6, 3)
Plot the points and sketch the graph.
We have the graph of the rational function below:
ANSWER:
Vertical asymptote: x = -4
Horizontal asymptote: y = 2