Question

The test scores for the analytical writingsection of a particular standardized test canbe approximated by a normal distribution, asshown in the figure.(a) What is the maximum score that can be inthe bottom 10% of scores?(b) Between what two values does the middle80% of scores lie?

Answer 1

Given:

Recall that the z-value is expressed as

Thus,

`z=(x-3.7)/(0.91)\text{ ---- equation 1}`

A) maximum score that can be in the bottom 10% of scores

using the table of z-values,

for the bottom 10% scores, we have

`z=-1.28155156554`

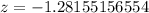
To evaluate x, substitute the value of z into equation 1.

Thus,

`\begin{gathered} -1.28155156554=(x-3.7)/(0.91)\text{ } \\ \Rightarrow x=2.5337895 \end{gathered}`

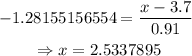
Thus, the maximum score that can be in the bottom 10% of scores is 2.5

B) Two values for which the middle 80% of scores lie.

From the z score values shown below:

The z scores of the value are

`\begin{gathered} z_1=-1.28 \\ z_2=1.28 \end{gathered}`

Thus,

`\begin{gathered} \text{when z=-1.28, we have} \\ -1.28=(x-3.7)/(0.91)\text{ } \\ \Rightarrow x=2.5352 \\ \text{when z=1.28, we have} \\ 1.28=(x-3.7)/(0.91) \\ \Rightarrow x=4.8648 \end{gathered}`

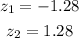
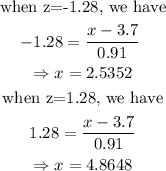
Thus, the two values for which the middle 80% of scores lie are 2.5 and 4.86.