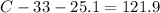ANSWER:
A=25.1 degrees
b = 1.8
C = 121.9 degrees
SOLUTION:
We can solve this problem using the cosine law, since we are given the length of 2 sides of triangle and the angle they formed.
![b\text{ =}\sqrt[]{c^2+a^2-2ac\cos B}](https://img.qammunity.org/2023/formulas/mathematics/college/uchsptwjeml7hz6zxgv7cmlxkluh3cdn00.png)
We substitute the given
![\begin{gathered} b\text{ =}\sqrt[]{(2\sqrt[]{2})^2+(\sqrt[]{2})^2-2(\sqrt[]{2})(2\sqrt[]{2})\cos 33} \\ b\text{ = 1.8} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f7j3s16pyf6f4g7v58cl5x76t2jvl44zoy.png)
Using Sine Law, we can get the angles
![\begin{gathered} (1.8)/(\sin 33)=\frac{\sqrt[]{2}}{\sin A} \\ A=25.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/anh0mxe7u3xp6azcz79v3bpb5nbn4x2gt3.png)
Since the total angle inside a triangle is 180, the angle at C is