Question

Solve the following system algebraically.y = x2 – 9x + 18y = x – 3Question 10 options:A) (3,0) and ( 4,2)B) (–4,5) and (7,–10)C) (3,1) and (5,3)D) (7,4) and (3,0)

Answer 1

`D\text{.}(7,4)\&(3,0)`

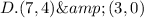
Step-by-step explanation

We want to solve the system of equations algebraically:

`\begin{gathered} y=x^2-9x+18 \\ y=x-3 \end{gathered}`

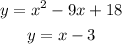
To solve this, let us substitute the second equation into the first equation.

That is:

`\begin{gathered} x-3=x^2-9x+18 \\ \Rightarrow x^2-9x-x+18+3=0 \\ x^2-10x+21=0 \end{gathered}`

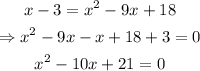
Now, we solve for x in the equation above by factorization:

`\begin{gathered} x^2-7x-3x+21=0 \\ x(x-7)-3(x-7)=0 \\ (x-3)(x-7)=0 \\ \Rightarrow x=3;x=7 \end{gathered}`

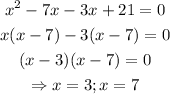
Finally, input the obtained values of x into the second equation to obtain y:

`y=x-3`

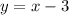
That is:

`\begin{gathered} \Rightarrow y=3-3 \\ y=0 \\ \Rightarrow y=7-3 \\ y=4 \end{gathered}`

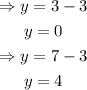
Therefore, the solutions to the system of equations are:

`(7,4);(3,0)`