Question

The maintenance department at the main campus of a large state university receives daily requests to replace fluorecent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 48 and a standard deviation of 3. Using the 68-95-99.7 rule, what is the approximate percentage of lightbulb replacement requests numbering between 45 and 48?Do not enter the percent symbol.ans =%

Answer 1

Solution.

`\begin{gathered} Given: \\ \mu=48 \\ \sigma=3 \end{gathered}`
`We\text{ can see that 45 = 48 - 3 that is, 45 is one standard deviation from mean in the left side . \lparen1\rparen}`

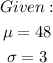
According to the 68-95-99.7% rule, 68% of the population falls within 1 standard deviation from the mean.

34% (half of 68%) of the population on right side and 34% population on the left side of the density curve. (2)

From (1) and (2), the approximate percentage of light bulb replacement requests numbering between 45 and 48= 34%