Question

Martin designed a bead that was a right cylinder with a cylindrical hole through the center of the bases. The outer cylinder had a radius of 1 centimeter, the inner cylinder had a radius of 0.5 centimeters, and the height of the bead was 1.5 centimeters. After creating the bead, he covered the entire bead with a protective coating.What was the approximate area of the bead that Martin covered?

Answer 1

We can make a skecth of the bead as:

Then, we can find the approximate area by listing all the areas that will be covered:

0. Area of the top (A1), that will be the area of the bigger circle minus the area of the smaller circle.

,

1. Area of the base (A2), equal to the area of the top (we can add them when calculating).

,

2. Lateral surface (A3) of the bigger cylinder.

,

3. Lateral surface (A4) of the inner cylinder.

Then, we can write the area A as the sum of the areas we have just listed:

`A=A_1+A_2+A_3+A_4`

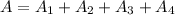
We can then write them in function of the radius and the height as

`\begin{gathered} A=A_1+A_2+A_3+A_4 \\ A=\pi(R^2-r^2)+\pi(R^2-r^2)+2\pi Rh+2\pi rh \end{gathered}`

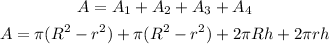
We can group the terms and replace the variables with their values and then solve:

Answer: the approximate area is 18.85 cm² (exact solution: 6π cm²)