Question

How to solve this equation? The WIDTH of a youth soccer field must be atleast 45 meters, but cannot exceed 60 meters. Write two inequalities that describe the width, w, of a youth soccer field. Then write two integers that are solutions of both inequalities.

Answer 1

Given that the width of a youth soccer field must be at least 45 meters, but cannot exceed 60 meters.

Let's write two inequalities that describe the width.

Let w represent the width,

Since the width must be at least 45 meters and not exceed 60 meters, that means it must not be less than 45 meters and must not be greater than 60 meters.

Hence, the first inequaity is:

`45\le w\le60`

Also, another way to write the inequality is:

`60\ge w\ge45`

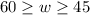
Now, let's write two intergers that are solutions to both inqualities.

For the first inequality, since w is greater than or equal to 45, one interger that is a solution is = 47

For the second inequality, since w is less that or equal to 60, one integer that is a solution is = 54

Therefore, two integers that are solutions of both inequalities are:

47 and 54

ANSWER:

• First inequality: ,45 ≤ w ≤ 60

,

• Second inequality: ,60 ≥ w ≥ 45

• Two solutions: 47 and 54