Question

A bag of marbles contains 2 white, 3black, 1 red, and 4 blue marbles. Cadedraws two marbles from the bag atrandom, one after the other. He replacesthem both and starts over. He does thisa total of 30 times.What is a reasonable prediction for thenumber of times he will draw a bluemarble followed by a black marble?

Answer 1

Write out the formula of Probability

`\text{Probability}=\frac{Number\text{ of favourable outcomes}}{Total\text{ number of outcomes}}`

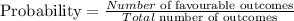
Let's get the total number of marbles= 2+3+1+4= 10marbles.

Let A represents blue marbles, A= 4.

Let B represents black marbles, B= 3

Let's get the probability of the blue marble

`P(A)=(4)/(10)=(2)/(5)`

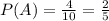
Let's get the probability of black marble

`P(B)=(3)/(10)`

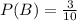
Let us now get the probability of blue marble and black marble

`\begin{gathered} P(A)\text{.P(B)}=(2)/(5)*(3)/(10)=(6)/(50)=(3)/(25) \\ P(A)\text{.P(B)}=(3)/(25) \end{gathered}`

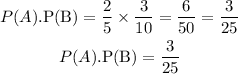
Hence the number of times he will draw a blue marble followed by a black marble is 3/25.