ANSWER:
![c=10\sqrt[]{6}\pi](https://img.qammunity.org/2023/formulas/mathematics/college/9rfririr4prk7bkuqmanco9zspw422anee.png)
Explanation:
To calculate the area of the entire circle we must do it by means of a proportion, since the entire circle is 360 °, therefore
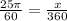
Solving for x:
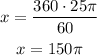
After calculating the area we can calculate the value of the radius, knowing that:
![\begin{gathered} A=\pi\cdot r^2 \\ \text{solving for r} \\ 150\pi=\pi\cdot r^2 \\ r=\sqrt[]{150} \\ r=5\sqrt[]{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tawb1w55ngzi4s0mbm3ybd14yl51fycu6o.png)
Now, the formula for the circumference is the following:
![\begin{gathered} c=2\pi r \\ c=2\pi\cdot5\sqrt[]{6} \\ c=10\sqrt[]{6}\pi \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6ojmj6h2y3vztt1f3ihbolv3vhbpr5zwvi.png)