The first measurement correspond to week=0, and the bee population is B(0)=500.
We can construct a table with the values as:
w | B(w)
0 | 500
1 | 1000
2 | 2000
3 | 4000
Each week, the bee population is growing by the same factor:
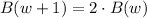
The bee population is doubling each week.
We can model this relation as an exponential growth:
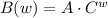
We can find the values of the parameters using the values from the graph:
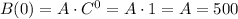
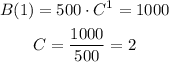
Then, the equation that relates bee population B and weeks w is:
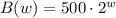
Answer:
1) 500
2) We can find that the population is doubling by calculating the ratio between the populaiton of consecutive weeks. The qoutient B(w+1)/B(w) is always equal to 2, so the bee population is doubling.
3) The equation is B(w) = 500*2^w