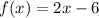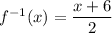Answer:
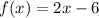
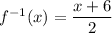
Explanation:
Using slope-intercept form of linear function:
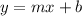
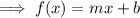
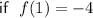
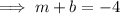
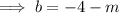
Find inverse of slope-intercept form:
swap x and y:
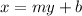
Make y the subject:
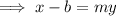
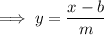
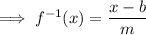
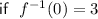

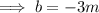
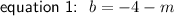
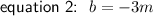
Equate the equations and solve for
 :
:
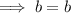
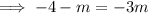
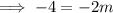
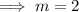
Substitute found value for
 into one of the equations and solve for
into one of the equations and solve for
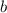 :
:
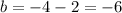
Substitute found values of
 and
and
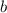 into equations for
into equations for
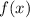 and
and
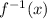 :
: