Question

Find the number of units of natural gas that are to be produced to maximize the profit if….

Answer 1

We are asked to determine the maximum value of "x" for a profit function given the functions of revenue and cost. To do that let's remember that profit is defined as:

`\text{Profit}=\text{revenue - cost}`

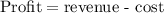
Let P(x) be the function of profit, then the difference between the functions of revenue and cost is the function of profit, therefore:

`P(x)=R(x)-C(x)`

Replacing the functions we get:

`P(x)=162x-2x^2-(x^2+114x+2)`

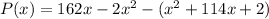
Now we apply the distributive property in the parenthesis:

`P(x)=162x-2x^2-x^2-114x-2`

Adding like terms:

`P(x)=48x-3x^2-2`

Now, to determine the maximum profit we will determine the derivative of the profit function with respect to "x":

`(dP)/(dx)=(d)/(dx)(48x-3x^2-2)`

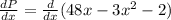
Now we distribute the derivative on the left side:

`(dP)/(dx)=(d)/(dx)(48x)-(d)/(dx)(3x^2)-(d)/(dx)(2)`

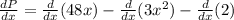
Now we determine the derivative using each corresponding rule:

`(dP)/(dx)=48-6x`

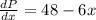
Now we set the result to zero:

`48-6x=0`

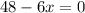
Now we solve for "x" first by subtracting 48 from both sides:

`-6x=-48`

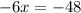
Now we divide both sides by -6:

`x=-(48)/(-6)=8`

Now, since the original function is a parabola that opens downwards, this point must be a maximum. To verify that we can determine the second derivative and we get:

`(d^2P)/(dx^2)=(d)/(dx)(48-6x)=-6`

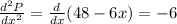
Since the second derivative is smaller than zero, the point is a maximum as hypothesized. Therefore, the maximum value of "x" is 8.