Question

iven the triangle ABC at points A = ( 2, 4 ) B = ( - 1, 3 ) C = ( - 4, 6 ), and if the triangle is first reflected over the y axis, and then over the x axis, find the new point A''.

Answer 1

Given a triangle, ABC, with the coordinates point A below

`A=(2,4)`

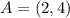
If the triangle is reflected over the y-axis first, the rule for the transformation is

`(x,y)\rightarrow(-x,y)`

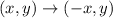
The coordinates of point A becomes,

`(2,4)\rightarrow(-2,4)`

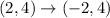
Then, the reflected over the x-axis, the rule for the transformation is

`(x,y)\rightarrow(x,-y)`

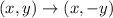
Then, the new point, A" will be

`(-2,4)\rightarrow(-2,-4)`

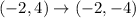
Thus, the answer is option d