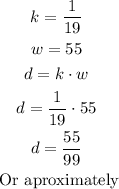From the first sentence of the exercise, we know that this is a question about direct variation. Then, we can write the following equation:

We can find the value of k replacing the known values in the above equation:

Now, we can find the new value of d replacing w = 55 and the found value of k in the initial equation: