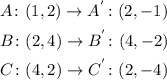For the first question, you can see in the graph that the triangle ABC has the coordinates
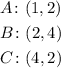
For the second question, you know that if the starting point has coordinates (x,y), a rotation of 90 degrees will have the coordinates (-y,x). So, the vertices of triangle A',B',C', the coordinates of triangle ABC after a rotation of 90 degrees will be
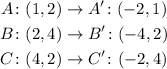
For the third question, you know that if the starting point has coordinates (x,y), a rotation of 180 degrees will have the coordinates (-x,-y). So, the vertices of triangle A'',B'',C'', the coordinates of triangle ABC after a rotation of 180 degrees will be
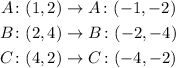
Finally, for the fourth question, you know that if the starting point has coordinates (x,y), a rotation of 270 degrees will have the coordinates (y,-x). So, the vertices of triangle A''',B''',C''', the coordinates of triangle ABC after a rotation of 270 degrees will be