The slope, m, of a line that passes through the points (x1, y1) and (x2, y2) is calculated as follows:

Line q passes through the points (0, 3) and (5, 0), then its slope is:
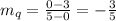
Line v passes through the points (0, -3) and (5, -6), then its slope is:
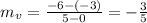
Since both lines have the slope of -3/5, lines q and v are parallel