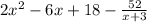Question

I am unsure of how to approach this equation. We are tasked with solving it using either Long Division or Synthetic Division.

Answer 1

1st step : Arrange the exponent of x of the dividend from highest to smallest.

Note that you need to add a term in between with 0 as coefficient.

`2x^3+2\Rightarrow2x^3+0x^2+0x+2`

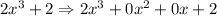
2nd step is to equate the divisor to zero and solve for x :

`\begin{gathered} x+3=0 \\ x=-3 \end{gathered}`

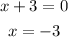
3rd step : Is to do synthetic division by using only the coefficients of the dividend and the value of x in the divisor.

Note that the operation in this process is multiplication and addition.

First is to bring down 2 and multiply it by -3, you will get -6 in the 2nd column.

Perform addition and multiply it again to -3 until the last term.

we have 2, -6, 18 and -52

These are the coefficients of the quotient.

and the variables will be :

`2x^2-6x+18`

we have a remainder of -52

To express the remainder as an algebraic expression, divide the remainder with the divisor.

and this will be :

`-(52)/(x+3)`

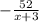
Putting all together, the answer is :

`2x^2-6x+18-(52)/(x+3)`