Question

How is this done please helpThe vertices of a figure are given. Rotate the figure as described. Find the coordinates of the image.

Answer 1

A'(1, -1), B'(6, 3), C'(6, -1)

Step-by-step explanation

We have triangle ABC, and we have to rotate it about vertex A 90 degrees counterclockwise,

Usually, when the center of rotation is the origin, the coordinates of each point exchange and the x-coordinate becomes negative (x, y) → (-y, x). But in this case, the center of rotation is A(1, -1).

If we translate the origin to point A, the new coordinates of the points would be,

Rotating these points about the new origin, the coordinates on the red coordinate plane are,

`\begin{gathered} A^(\prime)(0,0)\rightarrow A^(\prime)^(\prime)(0,0) \\ B^(\prime)(4,-5)\rightarrow B^(\prime)^(\prime)(5,4) \\ C^(\prime)(0,-5)\rightarrow C^(\prime)^(\prime)(5,0) \end{gathered}`

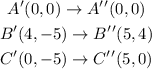
Let's graph these points,

Now, these points, in the original coordinate plane, have the coordinates,

Hence, the coordinates of the translated vertices are A'(1, -1), B'(6, 3), and C'(6, -1).