Question

Use the quadratic below to answer #2 and #3. 3x^2 + 2x = 22. What are the values of a, b, and c? 3. Solve for x.

Answer 1

Given:

`3x^2+2x=2`

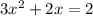
Question 2:

Let's find the values of a, b, and c.

Step 1:

Equate the equation to zero

Subtract 2 from both sides

`\begin{gathered} 3x^2+2x-2=2-2 \\ \\ 3x^2+2x-2=0 \end{gathered}`

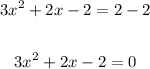
To find the values of a, b, and c, apply the general quadratic formula:

`ax^2+bx+c=0`

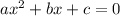
Comapre both equations:

`\begin{gathered} ax^2+bx+c=0 \\ 3x^2+2x-2=0 \end{gathered}`

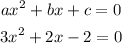
Thus, we have the following values:

a = 3

b = 2

c = -2

Question 3:

Let's solve for x

To solve for x, apply the formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Substitute 3 for a, 2 for b, and -2 for c:

`\begin{gathered} x=\frac{-2\pm\sqrt[]{2^2-4(3)(-2)}}{2(3)} \\ \\ x=\frac{-2\pm\sqrt[]{4-(-24)}}{6} \\ \\ x=\frac{-2\pm\sqrt[]{4+24}}{6} \\ \\ x=\frac{-2\pm\sqrt[]{28}}{6} \end{gathered}`

Solving further:

`\begin{gathered} x=(-2\pm5.29)/(6) \\ \\ x=(-2+5.29)/(6),\text{ }(-2-5.29)/(6) \\ \\ x=0.548,\text{ }-1.215 \end{gathered}`

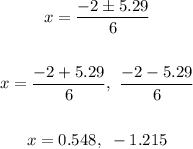
Therefore, the values of x are:

x = 0.548, -1.215

ANSWER:

2. a = 3, b = 2, c = -2

3. x = 0.548

x = -1.215