Question

Find the domain and range of the graphs. State the domain is discrete or continuous anddecide whether the graph is a function by a vertical line

Answer 1

The domain is the input or x-values for which a function is defined.

From the graph, the domain is the x-values of the points;

Therefore, the domain is;

`x=\mleft\lbrace0,1,2,3,4\mright\rbrace`

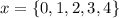
The range is the output or y-values for which a function is real and defined.

From the graph, the range is the y-values of the points;

Therefore, the range is;

`y=\mleft\lbrace0,2,4,6,8\mright\rbrace`

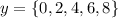
Since there are different points for the domain, therefore, the domain is not continuous.

Therefore, the domain is discrete.

Also, the graph is a function because, for every input, there is a corresponding single output.

It also passes the vertical line test, because if a vertical line is drawn across each point, it passes through one output (one y-value) only, hence it is a function

Therefore, the graph is a function.