The second equation already has the value of x isolated, so in order to solve the system by substitution, we can apply this value of x from the second equation in the first one:
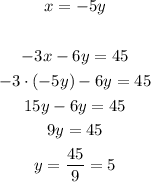
Now that we have the value of y, we can find the value of x:
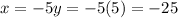
So we have that x = -25 and y = 5.