Question

Admission to a baseball game is $4.00 for general admission and $5.50 for reserved seats. The receipts were $5196.50 for 1181 paid admissions. How many of eachticket were sold?

Answer 1

Given:

Admission to a baseball game is $4.00 for general admission and $5.50 for reserved seats.

Let the number of tickets of general admission = x

Let the number of tickets of reserved seats = y

The receipts were $5196.50 ⇒ 4x + 5.5y = 5196.50

The paid admissions 1181 ⇒ x + y = 1181

So, we have the following system of equations:

`\begin{gathered} 4x+5.5y=5196.50\rightarrow(1) \\ x+y=1181\rightarrow(2) \\ \text{from}(2)\colon x=1181-y\rightarrow(3) \end{gathered}`

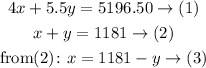
Substitute with x from (3) into (1) then solve to find y

`\begin{gathered} 4(1181-y)+5.5y=5196.50 \\ 4\cdot1181-4y+5.5y=5196.5 \\ 4724+1.5y=5196.50 \\ 1.5y=5196.50-4724 \\ 1.5y=472.5 \\ y=(472.5)/(1.5)=315 \end{gathered}`

Substitute with y into equation 3 to find x:

`x=1181-315=866`

So, the answer will be:

The number of tickets of general admission = 866

The number of tickets of reserved seats = 315