Question

Find the equation for the tangent to the curve of f at the point:f(x) = (3x+1)² , x = -1

Answer 1

The eqaution of the tangent at the point x = -1 is:

`y=-12x-8`

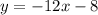
To solve this, first, we need to find the value of y when x = -1:

`f(-1)=(3\cdot(-1)+1)^2=(-3+1)^2=(-2)^2=4`

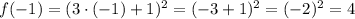
Then we want to find the equation of the tangent at the point (-1, 4)

The next step is to find the derivative of the equation, because the derivative thell us the slope of the tangent line at a certain point:

`\begin{gathered} f(x)=(3x+1)^2 \\ f^(\prime)(x)=2(3x+1)\cdot3=6(3x+1)=18x+6 \\ \\ f^(\prime)(x)=18x+6 \end{gathered}`

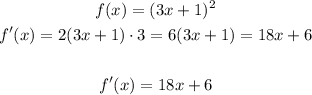
Now that we have the derivative, let's calculate the slope of the tangent like in the point (-1, 4). To do this, we evaluate the derivative in x = -1:

`f^(\prime)(-1)=18\cdot(-1)+6=-18+6=-12`

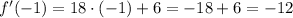
The slope of the tangent line is -12.

Now we have all the necessary things to construct the equation of a line: we have the slope (-12) and a point (-1, 4).

The slope-point form of a line is:

`\begin{gathered} y=m(x-x_0)+y_0 \\ \end{gathered}`

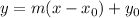
Where m is the slope and x0, y0 are the x and y coordinates of a point

Then:

`\begin{gathered} \begin{cases}m=-12 \\ x_0=-1 \\ y_0=4\end{cases} \\ y=-12(x-(-1))+4=-12\mleft(x+1\mright)+4=-12x-12+4=-12x-8 \end{gathered}`

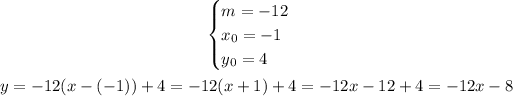
And that's the equation of the line y = -12x - 8