Question

Hello is it possible to receive help on this question?

Answer 1

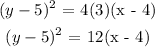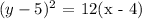
`(y-5)^2\text{ = 12(x - 4)}`Step-by-step explanation:

Vertex = (4, 5)

focuse = (7, 5)

The vertex and focus lie on the same horizontal line; y = 5

So we will be applying the equation of horizontal parabola

`\begin{gathered} \text{Equation of the parabola (horizontal):} \\ (y-k)^2=\text{ 4a(}x\text{ - h)} \end{gathered}`

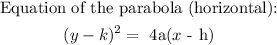
The focus lies on the right of the vertex, parabola opens upward as a result, a = positive

`\begin{gathered} As\text{ the y coordinates are the same, }a\text{ = 7 - 4 } \\ a\text{ = 3} \\ \\ \text{Vertex: h = 4, k = 5} \end{gathered}`

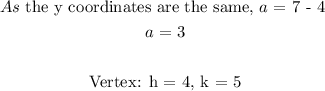
substituting the values:

`\begin{gathered} (y-5)^2\text{ = 4(3)(x - 4)} \\ (y-5)^2\text{ = 12(x - 4)} \end{gathered}`