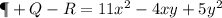To find what is P + Q - R
From the equation given
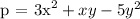
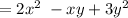
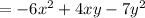
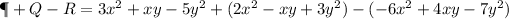
Now we will simplify the equation by first opening the parentheses
Values of Q will remain the same even after opening the parenthesis because it's addition but for the values of R, the signs will be affected because it's a subtraction.
That is :
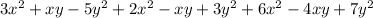
So the next is to rearrange them according to their powers
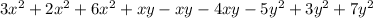
Then we will add or subtract variables that are the same accordingly(depending on their signs)
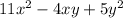
Therefore