Given the equation of the line:
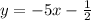
• You can identify that it is written in Slope-Intercept Form:

Where "m" is the slope of the line, and "b" is the y-intercept.
Notice that:
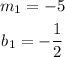
• By definition, parallel lines have the same slope, but their y-intercepts are different.
Therefore, you can determine that the slope of the line parallel to the first line is:
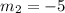
You know that this line passes through this point:
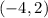
Therefore, substituting the slope and the coordinates of that point into this equation:
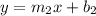
And solving for the y-intercept, you get:
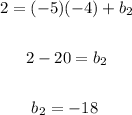
Then, the equation of the line parallel to the first line is:
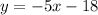
• By definition, the slopes of perpendicular lines are opposite reciprocal, therefore, the slope of this line is:
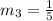
Using the same procedure used before to find the y-intercept, you get:
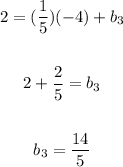
Therefore, its equation is:

Hence, the answer is:
- Equation for the parallel line:
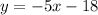
- Equation for the perpendicular line:
