We will determine the height of the tree as follows:
*First: We take the height of Dave to just ft, that is:
We know that one feet has 12 inches, so:

Now, we add that to the 6 feet:
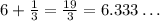
So, his height is 19/3 ft.
Now, we determine the height of the tree as follows:
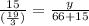
Here y represents the height of the tree, now we solve for it:
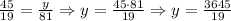

So, the height of the tree is approximately 191.8 feet.