To determine the points of intersection we first equate the expressions, then we solve for x. Once we have the values of x for which the functions are equal we plu them on one of the function to find its corresponding value of y.
a)
Let's equate the functions and solve for x:
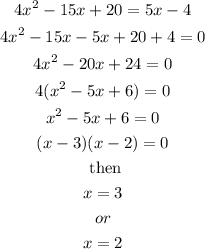
Now we find the corresponding values of y for each value of x; to do this we use the second equation.
When x=3:
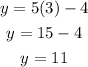
Hence the functions intersect at (3,11)
When x=2:
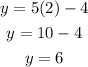
Hence the functions intersect at (2,6)
Therefore the function intersect at the points (3,11) and (2,6).
b)
Let's equate the functions and solve for x:
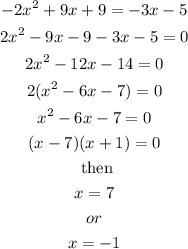
Now we find the corresponding values of y for each value of x; to do this we use the second equation.
When x=7:
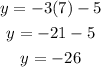
Hence the functions intersect at (7,-26)
When x=-1:
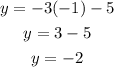
Hence the functions intersect at (-1,-2)
Therefore the function intersect at the points (7,-26) and (-1,-2).