Given
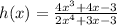
Find
Horizontal Asymptotes
Step-by-step explanation
As we know that there is two possible cases in arational function for there to be a horizontal asymptotes.
both depend on the higher degree of numerator and denominator.
1, if degree of denominator is equal to degree of numerator then there will be a horizontal asymptote at the ratio between the coefficients of the highest degree of the function.
2. if degree of denominator is lower to degree of numerator then there will be a horizontal asymptote at the y=0
here in given function degree of denominator is less than degree of numerator , so horizontal asymptote at y=0
Final Answer
horizontal asymptote at y=0