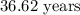The equation for the amount of money A in an account that earns interest compounded continuously, is:
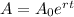
Where A_0 represents the initial deposit, r is the interest rate and t represents time.
If the annual interest is 3%, then the interest rate r is:
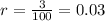
If the amount of money triples after a time t, then the savings account will be worth $3000 at that time. Substitute A=3000, A_0=1000 and r=0.03:
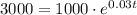
Isolate t to find the amount of time needed for the investment to triple:
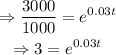
Take the natural logarithm to both sides of the equation:
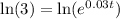
The natural logarithm of e^0.03t is equal to 0.03t. Then:
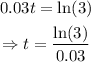
Use a calculator to evaluate the expression:
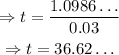
Therefore, to the nearest hundredth, the amount of time needed for the investment to triple, is: