Given that:
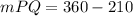
You get that its measure is:
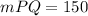
The exercise provides the formula for calculating the length of PQ:
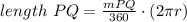
Where "r" is the radius of the circle.
Knowing that:
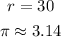
You can substitute values into the formula and then evaluate:
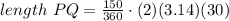
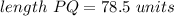
Hence, the answer is: Option C.