In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
f (x) = 3 / x + 4
g (x) = 7 / x + 1
(f ° g) (x) = ?
Step 02:
Composition rational functions:
(f ° g) (x) =
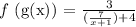
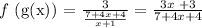
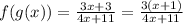
Domain of (f ° g) (x) :
4x + 11 = 0
4x = -11
x = -11/4 ===> Undefined point (singularity)
Domain:
(-oo , -11 /4) U ( -11/4 , oo)
The answer is:
(f ° g) (x) = 3(x + 1) / 4x + 11
Domain : (-oo , -11 /4) U ( -11/4 , oo)