Answer:
504 sq.in.
Explanation:
Given,
Edges of a box = 12 in. , 15 in. , 6 in.
So,
Lateral Surface Area (LSA) of the box
= 2 (l + b) h
- [On substituting their values]
= [2 (12 + 15) × 6 ]
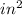
= [2 × 27 × 6]
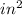
= 324
And,
Base area of the box
= l × b
- [On substituting the values]
= (12 × 15)
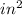
= 180
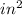
Therefore,
Total area painted by Agnes leaving the top of the box
= LSA of the box + Base area of the box
- [On putting their values]
= 324
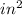 + 180
+ 180
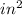
= 504
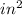
Hence,
The total area painted is 504
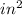 (Ans)
(Ans)