Question

Please help with math homework! Fifth Tudor I have had to get

Answer 1

Given the Amount compounded for one year as

`A=P(1\text{ + }(r)/(100))^t`

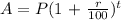
Where A is the amount at the end of one year

P is the amount invested

r is the rate of compound interest

t is the duration of investment( one year)

Let the three investstment be named A, B, and C, such that the interest I on A, B and C sum up to 32000.

`\begin{gathered} I_A+I_B+I_C=32,000\text{ ---- equation 1} \\ P_A+P_B+P_C=1,000,000\text{ ---- equation 2} \\ \end{gathered}`

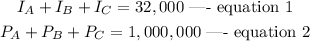
Investment A:

`\begin{gathered} A_{A_{}}=P_A(1+0.04)^1 \\ A_{A_{}}=P_A(1.04)^{}\text{ ---- equation 3} \end{gathered}`

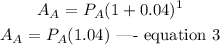
Investment B:

`\begin{gathered} A_{B_{}}=P_B(1+0.02)^1 \\ A_B=P_B(1.02)\text{ ---- equation 4} \end{gathered}`

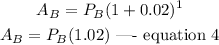
Investment C:

`\begin{gathered} A_C=P_C(1+0.06)^1 \\ A_C=P_C(1.06)\text{ ----- equation 5} \end{gathered}`

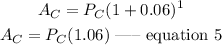
Meanwhile, the amount invested on A is four times that of C. this is given as

`P_A=4* Pc\text{ ----- equation 6}`

But

`I\text{ = A - P}`

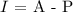
Thus, from equation 1, we have