Question

The product of two powers is 11^8 and their quotient is 11² what are the two powers? explain.

Answer 1

The two powers are 5 and 3

Step-by-step explanation

Given that;

The product of two powers is 11^8

The quotient of two power is 11^2

Follow the steps below to find the unknown powers

Let the unknown powers be x and y

Step 1; Apply the law of indicies

`\begin{gathered} \text{ x}^a\text{ }*\text{ x}^b\text{ = x}^{a\text{ + b}}\text{ --------- 1} \\ \text{ x}^a\text{ }/\text{ x}^b\text{ = x}^{a\text{ - b}}\text{ --------- 2} \end{gathered}`

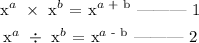
Since the product of the two powers is 11^8, then we have below equation

`\begin{gathered} \text{ 11}^8\text{ = 11}^x\text{ }*\text{ 11}^y\text{ = 11}^{x\text{ + y}} \\ \text{ 11}^8\text{ = 11}^{x\text{ + y}} \\ \text{ Since both sides of the equation have the same base, then, we have} \\ \text{ 8 = x + y ---------- equation 1} \end{gathered}`
`\begin{gathered} \text{ 11}^2\text{ = 11}^x\text{ }/\text{ 11}^y\text{ = 11}^{x\text{ - y}} \\ \text{ 11}^2\text{ = 11}^{x\text{ - y}} \\ \text{ Since both sides of the equation have the same base, then we have} \\ \text{ 2 = x - y ---------- 2} \end{gathered}`

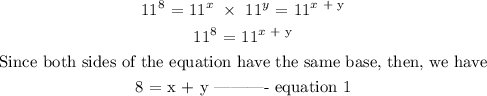
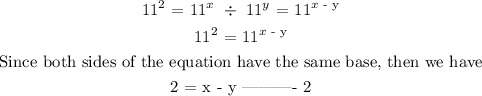
Step 2; Solve the two equations simultaneously to find the value of x and y

x + y = 8 ----------- equation 1

x - y = 2 ------------ equation 2

Isolate x in equation 1

x + y = 8

x = 8 - y -------- equation 3

Substitute x = 8- y into equation 2

8 - y - y = 2

8 - 2y = 2

Subtract 8 from both sides of the equation

8 - 8 - 2y = 2 - 8

-2y = -6

Divide both sides by -2

y = -6/-2

y = 3

Find the value of x by substituting y = 3 into equation 1

x + y = 8

x + 3 = 8

x = 8 - 3

x = 5

Therefore, x = 5 and y = 3

Hence, the two powers are 5 and 3