Question

A technical machinist is asked to build a cubical steel tank that will hold 220 L of water.Calculate in meters the smallest possible inside length of the tank. Round your answer to the nearest 0.001 m.

Answer 1

As per given by the question,

The given value is 220 L, i.e volume.

Now,

There is need to calculatea cube volume.

So,

Cube volume is calculated by multiplying the lenght cube .

That means,

`(\text{length)}^3`

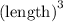
Then,

The volume of the tank is 220 L.

So,

From the formula of volume,

`V=R^3`

Then,

`\begin{gathered} V=R^3 \\ 220=R^3 \\ R=\sqrt[3]{(220)/(1000)} \end{gathered}`

Then, according to properties;

`\begin{gathered} 1L=(1)/(1000)m^3,\text{ so} \\ 220L=(220)/(1000) \end{gathered}`

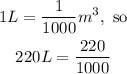
Then,

`\begin{gathered} R=\sqrt[3]{(220)/(1000)} \\ R=6.0368 \end{gathered}`

Now,

For the nearest 0.001,

`\begin{gathered} R=(6.0368)/(10)m \\ R=0.6038 \end{gathered}`

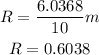
Hence, the smallest possible inside length is 0.604.