Question

Drag and drop an answer to each box to correctly complete the explanation for deriving the formula for the volume ofa sphere.For every corresponding pair of cross sections, the area of the cross section of a sphere with radius r is equalto the area of the cross section of a cylinder with radius r and height 2r minus the volume of two cones, eachwith a radius and height ofA cross section of the sphere isof the cylinder minus the cones, taken parallel to the base of cylinder, isThe volume of the cylinder with radius r and height 2r isvolume of the sphere isand a cross sectionradius r and height ris ³. So the volume of the cylinder minus the two cones is ³. Therefore, theby Cavalieri's principle.and the volume of each cone with

Answer 1

For every corresponding pair of cross sections, the area of the cross section of a sphere with radius r is equal to the area of the cross section of a cylinder with radius r and height 2r minus the volume of two cones, each with a radius and height of r. A cross section of the sphere is a circle, and a cross section of the cylinder minus the cones, taken parallel to the base of cylinder, is an annulus. The volume of the cylinder with radius r and height 2r is
`2\pi r^3`, and the volume of each cone with radius r and height r is
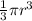`(1)/(3) \pi r^3`. So the volume of the cylinder minus the two cones is
`(4)/(3) \pi r^3`. Therefore, the volume of the sphere is
`(4)/(3) \pi r^3` by Cavalieri's principle.

In Mathematics and Euclidean Geometry, the volume of a sphere can be calculated by using the following mathematical equation (formula):

Volume of a sphere =
`(4)/(3) \cdot \pi r^3`

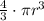
Where:

r represents the radius.

Cavalieri's principle states that two geometric figures would have the same volume when they have the same height and the same cross-sectional area (CSA) at every point along that height.

By Cavalieri's principle, a sphere and a cylinder with two cones removed have equal volumes. The volume of the cylinder with radius r and height 2r is
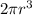`2 \pi r^3` while the volume of each cone with radius r and height r is
`(1)/(3) \pi r^3`.

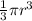Furthermore, the volume of the cylinder with two cones removed is
`(4)/(3) \pi r^3`. Therefore, the volume of the sphere is
`(4)/(3) \pi r^3`.

Answer 2

Given:

For every corresponding pair of cross sections, the area of the cross-section of a sphere with radius r is equal to the area of the cross-section of a cylinder with radius r and height 2r minus the volume of two cones, each with a radius and height of .....

Required:

We need to find the height of the given cone.

Step-by-step explanation:

Recall that Cavalieri's principle tells us that if 2 figures have the same height and the same cross-sectional area at every point along that height, they have the same volume.

The area of the cross-section of the sphere is an area of the circle with a radius r.

`A=\pi r^2`

The area of the cross-section of the cylinder is again area of the circle with radius r.

We know that the volume of the two cones is equal.

So the radius and height of the cone is r.

Final answer: