Question

Find the volume of the pyramid. Example 1 I need a better explanation for this problem.

Answer 1

36 m³

Step-by-step explanation:

The volume of the pyramid can be calculated as

`V=B\cdot h\cdot(1)/(3)`

Where B is the area of the base and h is the height of the pyramid. In this case, the height of the pyramid is 9 m, so, we will need to replace h = 9 m

The base of the pyramid is a triangle, so the area of the base is

`\begin{gathered} B=(1)/(2)\cdot base\text{ of triangle}\cdot height\text{ of triangle} \\ \\ B=(1)/(2)\cdot4\cdot6 \\ \\ B=(1)/(2)\cdot24 \\ \\ B=12 \end{gathered}`

Then, replacing B = 12 and h = 9, we get that the volume of the pyramid is

`\begin{gathered} V=12\cdot9\cdot(1)/(3) \\ \\ V=108\cdot(1)/(3) \\ \\ V=36 \end{gathered}`

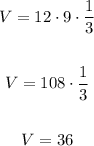
Therefore, the volume is 36 m³