Question

What is the system of inequalities associated with the following graph?A) {y>−2 {x+y≥1 B) {y<−2 {x+y≥1 C) {y<−2 {x+y<1 D) { y< -2 { x + y>1

Answer 1

We have the following graph representing the solution for two inequalities:

And we have to determine the system of inequalities that corresponds to that graph.

To determine the system of inequalities that corresponds to the given graph, we can proceed as follows:

1. Find the equations that correspond to the two lines. For this, we have that one of the lines (the dotted line) has the following equation:

`y=-2`

Since it is a horizontal line.

2. The other line can be found by using the two intercepts of this line: (0, 1), the y-intercept, and (1, 0), the x-intercept. Then, by using the two-point form of the line equation, we have:

We can label these two points as follows:

• (0, 1) ---> x1 = 0, y1 = 1

,

• (1, 0) ---> x2 = 1, y2 = 0

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ \\ y-1=(0-1)/(1-0)(x-0) \\ \\ y-1=(-1)/(1)x=-x \\ \\ y-1=-x \\ \\ y=-x+1 \end{gathered}`

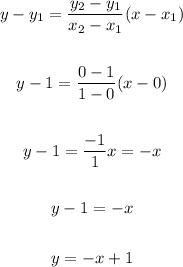
3. Now, we have the following two equations:

`\begin{gathered} y=-2 \\ \\ y=-x+1 \end{gathered}`

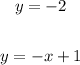
4. To find the corresponding values for the inequalities, we can see that both inequalities do not have a point (0, 0) as a solution. Then we have to find the corresponding symbol for the inequality:

`\begin{gathered} (0,0)\rightarrow y=-x+1\Rightarrow0=-(0)+1\Rightarrow0=0+1\Rightarrow\text{ For this to be true:} \\ \\ 0\leq1\rightarrow\text{ Notice the equal symbol. This is because we have a solid line } \\ \text{ representing the inequality.} \\ \text{ Since \lparen0, 0\rparen is NOT a solution, then the inequalty is the opposite of the one} \\ \text{ we got. Then the inequality is of the form:} \\ \\ y\ge-x+1 \end{gathered}`

And the other inequality is of the form:

`\begin{gathered} \text{ For \lparen0, 0\rparen, we have:} \\ \\ y=-2\Rightarrow0>-2.\text{ Since \lparen0,0\rparen is NOT a solution, then the inequality is of } \\ \text{ the form:} \\ \\ y<-2\rightarrow\text{ Notice that, since we have a dotted line, the inequality does not } \\ \text{ have the equal sign.} \\ \end{gathered}`

5. Therefore, the system of the inequalities is given by:

`\begin{gathered} \begin{cases}y<-2 \\ y\ge{-x+1=y+x\ge1=x+y\ge1}\end{cases} \\ \\ \end{gathered}`

Therefore, in summary, the system of inequalities associated with the graph is:

`\begin{cases}y<{-2} \\ x+y\ge1\end{cases}`

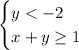
[Option B]