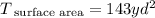We have the following solid:
And we have to find the surface area of that solid.
We can see some tick marks that tell us that the corresponding sides are congruent, that is, the sides have the same length. To find this surface area we can calculate the area of each of the figures that compose the solid, that is:
• Two congruent trapezoids
,
• Two congruent rectangles
,
• Two different rectangles
Then we can proceed as follows:
Finding the area for the two congruent trapezoids
1. We can see from the figure the following trapezoid:
2. And we have that the measures of this trapezoid are:
• Small base (base 1, b1) = 3yd
,
• Large base (base 2, b2) = 7yd
,
• Height (h) = 3.5yd
3. Now, the area of a trapezoid is given by:
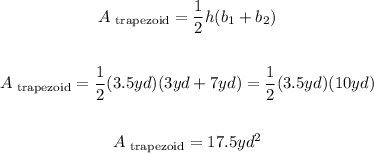
4. Since we have two congruent trapezoids, then we have that the area for them is:

Therefore, the total area for the trapezoids is 35 square yards.
Finding the area for the two congruent rectangles
5. We need to find the area of these two rectangles:
6. And the area of each of them is given by:
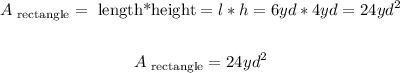
7. Then the area of both rectangles is:
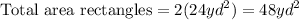
Therefore, the total area of the congruent rectangles is 48 square yards.
Finding the areas of the lower rectangle and the upper rectangle
8. These two rectangles are:
9. Then the corresponding areas are:
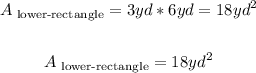
10. And

Therefore, the area of the lower rectangle is 18 square yards, and the area of the upper rectangle is 42 square yards.
Total Surface Area
Now, the total surface area of the solid is the sum of all the resulting areas above:
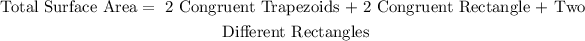
Then we have:
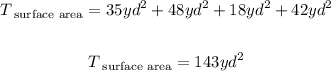
Therefore, in summary, the surface area is equal to 143 square yards (last option):