The Hypotenuse-Leg Theorem states that two right triangles are congruent if and only if the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of the other right triangle.
Using this theorem in our problem, we get the following two equations
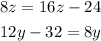
Solving the first equation we have
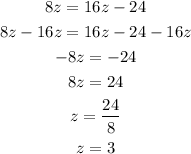
The value for z is 3.
Solving the second equation, we have
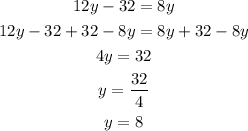
The value for y is 8.