The total cost has two parts:
- a fixed one for the entry, $5
- a variable one, $1 per ticket.
If y is the total cost and x is the number of tickets, then y will be the sum of the fixed cost and the variable cost multplyied by the number of tickets, x.
That is, the equation is:

Using this equation, we can calculate y for each x in the table.
For x = 0:

For x = 1:
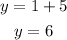
For x = 2:

For x = 5:
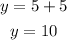
So, the table is:
x | # tickets | 0 | 1 | 2 | 5
y | cost | 5 | 6 | 7 | 10
For the graph, we can plot at least two of these points and connect them to form a line: