The diagram showing the setup in the question is shown below:
We can use the Pythagorean Theorem to solve for the length of the rope:
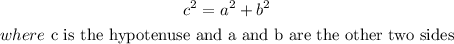
From the diagram, we have the following parameters:
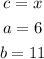
Therefore, the length of the rope is calculated to be:
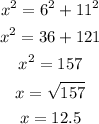
The length of the rope is 12.5 meters.