Question

A mass M=7kg hangs on the end of a massless rope with L=2.11m long. The pendulum is held horizontal and released from rest. Then a peg is placed 4/5 of the way down the pendulum’s path so that when the mass falls to its vertical position it hits and wraps around the peg. As it wraps around the peg and attains it’s maximum height it ends a distance of 3/5*L below its starting point ( or 2/5*L below its lowest point. 1) How fast is the mass moving at the top of its new path ( directly above the peg)?2) using the original mass M=7kg, what is the magnitude of the tension in the string at the top of the new path (directly above the peg)?

Answer 1

Part (1)

The height of mass at the top of its new path is 2/5 L, therefore, the potential energy of the mass can be expressed as,

`U=\text{mg(}(2)/(5)L)`

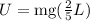
The kinetic energy of the mass can be given as,

`K=(1)/(2)mv^2`

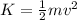
According to conservation of energy,

`U=K`

Plug in the known values,

`\begin{gathered} mg((2)/(5)L)=(1)/(2)mv^2 \\ v^2=(4)/(5)gL \\ v=\sqrt[]{(4)/(5)gL} \end{gathered}`

Substitute the known values,

`\begin{gathered} v=\sqrt[]{(4)/(5)(9.8m/s^2)(2.11\text{ m)}} \\ \approx4.07\text{ m/s} \end{gathered}`

Thus, the speed of mass at the top of its new path is 4.07 m/s.

Part (2)

The tension in the string can be given as,

`T=-Mg+F`

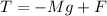
The centripetal force acting on the mass is,

`F=(Mv^2)/(((2)/(5)L))`

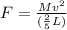
Therefore, the tension in the string becomes,

`\begin{gathered} T=-Mg+(Mv^2)/(((2)/(5)L)) \\ =-Mg+(5)/(2)(Mv^2)/(L) \end{gathered}`

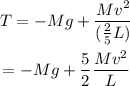
Substitute the known values,

`\begin{gathered} T=-(7kg)(9.8m/s^2)(\frac{1\text{ N}}{1kgm/s^2})+(5)/(2)\frac{(7kg)(4.07m/s)^2}{(2.11\text{ m)}}(\frac{1\text{ N}}{1kgm/s^2}) \\ =-68.6\text{ N+}137.4\text{ N} \\ =68.8\text{ N} \end{gathered}`

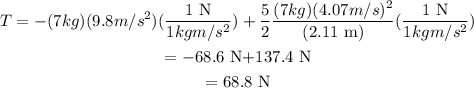
Thus, the tension in the string is 68.8 N.