Question

Wat is 24,12,6 to the 8th term. Round it to the nearest 1000

Answer 1

We can see that 24 divided by 2 is 12. Similarly, 12/2 is 6 and so on. Then, the sequence rule can be written as

`a_n=24((1)/(2))^(n-1)_{}`

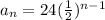
For instance,

`\begin{gathered} a_1=24((1)/(2))^(1-1)=24((1)/(2))^0=24*1=24 \\ a_2=24((1)/(2))^(2-1)=24((1)/(2))=12 \\ a_3=24((1)/(2))^(3-1)=24((1)/(4))=6 \end{gathered}`

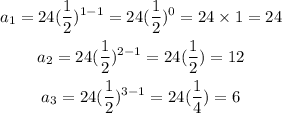
Then, by substituting n=8 (8th term) into the first equation, we have

`a_8=24((1)/(2))^(8-1)=24((1)/(2))^7=24*(1)/(128)=0.1875`

therefore, by rounding to the nearest thousandth, the answer is 0.188.