Question

What is the solution to the inequality 7x^2 + 35x > 42?

Answer 1

In order to find the solution of this inequality, first let's find its roots:

`\begin{gathered} 7x^2+35x=42 \\ 7x^2+35x-42=0 \\ x^2+5x-6=0 \\ a=1,b=5,c=-6 \\ \\ x_1=\frac{-b+\sqrt[]{b^2-4ac}}{2a}=\frac{-5+\sqrt[]{25-4\cdot1\cdot(-6)}}{2}=\frac{-5+\sqrt[]{49}}{2}=(-5+7)/(2)=1 \\ x_2=\frac{-b-\sqrt[]{b^2-4ac}}{2a}=(-5-7)/(2)=-6 \end{gathered}`

The roots are 1 and -6.

Since the concavity of this function is upwards (because a > 0), we have that the function is negative for value of x between the roots and positive for the other values (x < -6 or x > 1).

Since the inequality has the symbol "greater than or equal", we want the positive values, including zero, therefore the answer is x ≤ -6 or x ≥ 1 (option B).

Answer 2

`x < - 6 \ \text{and} \ x > 1`

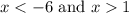
Explanation:

Givens

We are given an inequality:

`7x^2 + 35x > 42`

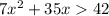
We are asked to find the solution to this inequality.

Solve

First, treat this as a quadratic equation. Get the inequality to quadratic form:

`ax^2+bx+c > 0\\\\7x^2+35x > 42\\\\7x^2+35x-42 > 42-42\\\\7x^2+35x-42 > 0`

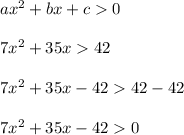
Then, divide both sides by 7:

`\displaystyle 7x^2+35x-42 > 0\\\\(7x^2+35x-42)/(7) > (0)/(7)\\\\x^2+5x-6 > 0`

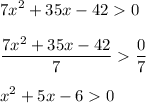
Then, separate 5x to create a factorable expression. Ask yourself: what two numbers will add up to -6 and multiply to create -6?

`x^2+5x-6 > 0\\\\x^2+6x-x-6 > 0`

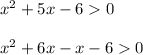
Then, group the terms together:

`x^2+6x-x-6 > 0\\\\(x^2+6x)(-x-6) > 0`

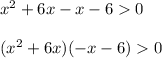
Then, factor out x from the inequality:

`(x^2+6x)(-x-6) > 0\\\\x(x+6)(-x-6) > 0`

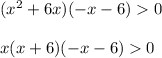
Then, factor out the negative sign from the second part of the expression:

`x(x+6)(-x-6) > 0\\\\x(x+6)-(x+6) > 0`

Then, factor out x + 6 from the inequality:

`x(x+6)-(x+6) > 0\\\\(x+6)(x-1) > 0`

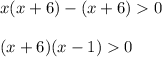
Then, separate the factors and create two separate inequality sets:

`(x+6)(x-1) > 0\\\\\displaystyle \left \{ {{x+6 > 0} \atop {x-1 > 0}} \right. \\\\\left \{ {{x+6 < 0} \atop {x-1 < 0}} \right.`

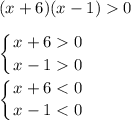
Then, solve the inequalities for x:

`x+6 > 0\\\\x+6-6 > 0-6\\\\x > -6\\---------------\\x-1 > 0\\\\x-1+1 > 0+1\\\\x > 1\\---------------\\x+6 < 0\\\\x+6-6 < 0-6\\\\x < -6\\---------------\\x-1 < 0\\\\x-1+1 < 0+1\\\\x < 1`

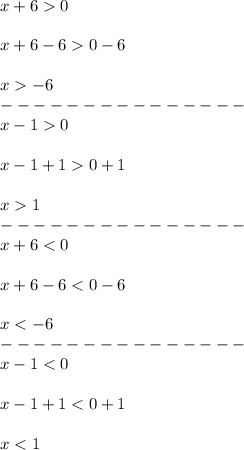
Then, test each value in the inequality:

`7x^2+35x > 42\\\\7(-5)^2+35(-5) > 42\\\\7(25)-175 > 42\\\\175-175 > 42\\\\0 \\gtr 42\\\\\text{x} > \text{-6 is not a solution.}\\---------------\\7x^2+35x > 42\\\\7(2)^2+35(2) > 42\\\\7(4)+70 > 42\\\\28+70 > 42\\\\98 > 42\\\\\text{x} > \text{1 is a solution.}\\---------------`

`\\7x^2+35x > 42\\\\7(-7)^2+35(-7) > 42\\\\7(49)-245 > 42\\\\343-245 > 42\\\\98 > 42\\\\\text{x} < \text{-6 is a solution.}\\---------------\\7x^2+35x > 42\\\\7(-1)^2+35(-1) > 42\\\\7(1)-35 > 42\\\\7-35 > 42\\\\-28\\gtr42\\\\\text{x} < \text{1 is not a solution.}`

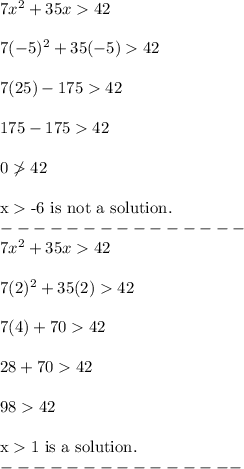
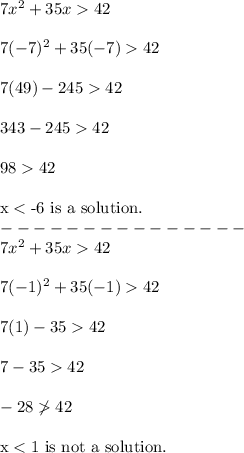
Final Answer

Therefore, the solutions are x > 1 and x < -6. This means that answer choice A is correct.