Given the functions:
![\begin{gathered} f(x)=\sqrt[3]{2x} \\ g(x)=2x+1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9rugw7sp1035xaef7kz96wyhs6cbtfe7nq.png)
then the quotient f/g is:
![((f)/(g))(x)=(f(x))/(g(x))=\frac{\sqrt[3]{2x}}{2x+1}](https://img.qammunity.org/2023/formulas/mathematics/college/wtc48m4iqop8uzq2o12z9o80s80cbc4u59.png)
then, notice that the cubic root of 2x is always defined for any real number, then, the domain will be all real numbers except the value that makes 2x+1 = 0, then:
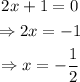
therefore, the domain is all real numbers except -1/2