Question

Hi thank goodness yea I am and thank

Answer 1

We are given the first derivative

`(di)/(dt)=210\sin(17.5t)`

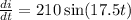
To find the antiderivative, we must think of functions whose derivative is sin x. That happens when we have f(x) = cos u. Recall:

`(d)/(dx)\cos u=-u^(\prime)\sin u`

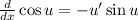
So we can assume that:

`-u^(\prime)\sin u=210\sin17.5t`

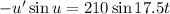
So we know that u must be 17.5t, which gives us u' = 17.5. Therefore there must be a multiplier before u' for us to get -210.

`-210/17.5=-12`

So, the antiderivative must be:

`i(t)=-12\cos(17.5t)+c`

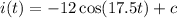
Let's check:-

`\begin{gathered} i(t)=-12\cos(17.5t)+c \\ \\ i^(\prime)(t)=-12(-17.5)[\sin(17.5t)]+0 \\ \\ i^(\prime)(t)=210\sin(17.5t) \end{gathered}`

To find the value of c, we will use i(0) = 0.

`\begin{gathered} i(t)=-12\cos(17.5t)+c \\ i(0)=-12\cos(17.5\cdot0)+c \\ 0=-12\cos0+c \\ 0=-12\cos0+c \\ 0=-12(1)+c \\ 0=-12+c \\ c=12 \end{gathered}`

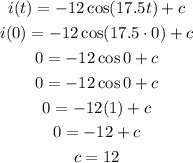
The complete equation for i(t) is:

`i(t)=-12\cos(17.5t)+12`

Using the equation we found for 1(t), we can calculate i(5).

`\begin{gathered} i(t)=-12\cos(17.5t)+12 \\ i(5)=-12\cos(17.5\cdot5)+12 \\ i(5)=-12(0.0436)+12 \\ i(5)=1.98 \end{gathered}`

The current when t = 5 is 1.98 amperes.

To find the time when the current is zero again, we substitute once more.

`\begin{gathered} i(t)=-12\cos(17.5t)+12 \\ 0=-12\cos(17.5t)+12 \\ -12=-12\cos(17.5t) \\ 1=\cos(17.5t) \\ \cos^(-1)1=17.5t \\ 2\pi=17.5t \\ t=0.359 \end{gathered}`

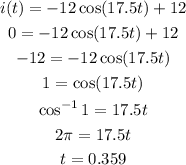
The next time that current is zero again is at t = 0.359 seconds.

The rate of change of di/dt when t = 0.5 is equal to its derivative (the second derivative of the original function).

`\begin{gathered} (di)/(dt)=210\sin(17.5t) \\ \\ (di^2)/(dt^2)=210(17.5)\cos(17.5t) \\ \\ (d\imaginaryI^(2))/(dt^(2))=3,675\cos(17.5t) \\ \\ (d\imaginaryI^(2))/(dt^(2))=3,675\cos(17.5\cdot0.5) \\ \\ (d\imaginaryI^(2))/(dt^(2))=3,675(0.988) \\ \\ \frac{d\mathrm{i}^2}{dt^2}=3,632 \end{gathered}`

The rate of change of di/dt at t = 0.5 is 3,632 amps/second^2.