Question

In the diagram shown below, triangle JKN ~ triangle NKM ~ triangle MKL.A) What is the length, in units, of NK?B) What is the length, in units, of NM? Show your work. Explain your reasoning.C) Prove that the measure of angle JKL is 90 degrees

Answer 1

A) NK = 6 units

B) NM = 2√3 units

Explanations:

A) According to the question, all the triangles are similar to one another. Taking the ratio of the similar sides of triangle JKN and triangle MKL, we will have:

`\begin{gathered} (JN)/(NK)=(ML)/(LK) \\ (3)/(NK)=(4)/(8) \\ 4NK=3(8) \\ 4K=24 \\ NK=(24)/(4)=6units \end{gathered}`

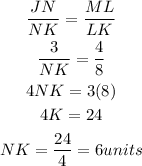
Therefore the measure of NK is 6 units

B) Taking the ratio of similar sides of triangle NKM and triangle MKL

`\begin{gathered} (NM)/(MK)=(ML)/(KL) \\ (NM)/(MK)=(4)/(8) \end{gathered}`

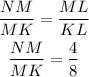
Determine the measure of MK using SOH CAH TOA

`\begin{gathered} sin\angle MLK=(MK)/(LK) \\ sin60=(MK)/(8) \\ MK=8sin60 \\ MK=8*(√(3))/(2) \\ MK=4√(3)units \end{gathered}`

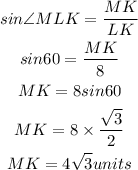
Substitute the result into the ratio above;

`\begin{gathered} (NM)/(MK)=(4)/(8) \\ (NM)/(4√(3))=(4)/(8) \\ NM=(16√(3))/(8) \\ NM=2√(3)units \end{gathered}`

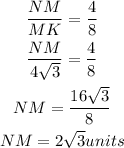
Hence the measure of length NM is 2√3 units

C) Since triangle JKN ~ triangle NKM ~ triangle MKL, hence Hence;