Question

X and y table graphgiven equation y=x squared - 12 x +36x: ? ,5,?,9,4y: 0,?,1,?,?

Answer 1

The table of values we need to complete is:

x y

? 0

5 ?

? 1

9 ?

4 ?

The given function is:

`y=x^2-12x+36`

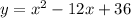
The procedure we will follow is to take the values from the table, x or y, and put them in the equation to find the missing values.

Step 1. In the first row of the table, the x is the unknown value and y=0.

Substitute y=0 into our equation:

`0=x^2-12x+36`

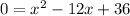
We have a quadratic equation that we can factor to solve for x.

The process to factor this kind of expressions is:

• Open two pairs of parentheses

,

• put x on each pair of parentheses

,

• find two numbers that when you multiply them the result is +36 and when you add them the result is -12

,

• add those numbers to the parentheses

In this case, the numbers are -6 and -6 because

(-6)*(-6)=36

-6+(-6)=-12

Thus, the factored expression is:

`(x-6)(x-6)=0`

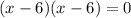
or we can simplify it to:

`(x-6)^2=0`

And solving for x:

`\begin{gathered} x-6=0 \\ x=6 \end{gathered}`

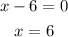
Updating the table:

x y

6 0

5 ?

? 1

9 ?

4 ?

Step 2. The second row has x=5 and y is the unknown value.

Substitute x=5 into the equation:

`\begin{gathered} y=x^2-12x+36 \\ y=5^2-12\cdot5+36 \\ y=25-60+36 \\ y=1 \end{gathered}`

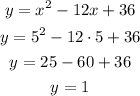
We keep updating the table with the new value of y:

x y

6 0

5 1

? 1

9 ?

4 ?

Step 3. The next row has y=1 and we need to find x.

Substitute y=1 into the equation:

`x^2-12x+36=1`

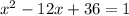
To solve by using the process from step 1, first, we need to make this equation equal to 0. For that reason we subtract 1 from both sides of the equation:

`\begin{gathered} x^2-12x+36-1=1-1 \\ x^2-12x+35=0 \end{gathered}`

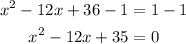
And following the same process from step 1, we factor the equation.

In this case, the numbers for the factorization will be -5 and -7 because:

(-5)(-7)=35

and

-5+(-7)=-12

And thus, the factored expression is:

`(x-5)(x-7)=0`

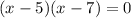
Here we will find two x values:

One equaling x-5 to 0

and the other equaling x-7 to 0.

The result for the x-values are:

`\begin{gathered} x-5=0\longrightarrow x=5 \\ x-7=0\longrightarrow x=7 \end{gathered}`

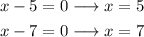
Thus, for y=1 we have two possible x values 5 and 7. Updating the table:

x y

6 0

5 1

5 and 7 1

9 ?

4 ?

Step 4. Find the y value when the x value is x=9.

Substitute x=9 into the equation:

`\begin{gathered} y=9^2-12\cdot9+36 \\ y=81-108+36 \\ y=9 \end{gathered}`

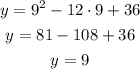
Updating the table:

x y

6 0

5 1

5 and 7 1

9 9

4 ?

Step 5. Find the y-value when the x value is 4.

Substitute x=4:

`\begin{gathered} y=4^2-12\cdot4+36 \\ y=16-48+36 \\ y=4 \end{gathered}`

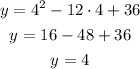
And we update the table for the last time:

x y

6 0

5 1

5 and 7 1

9 9

4 4

Answer:

x y

6 0

5 1

5 and 7 1

9 9

4 4